Deep learning is a powerful machine learning approach exploiting neural networks with various layers and shows outstanding performance in many fields including pattern recognition in imaging tasks. Finding correlations in image data that link image results to other diagnostic findings are at the heart of the use of this technology. Astonishing deep learning results range from image classification and object detection to beating world-class go players. Using convolutional and multi-scale networks, it could be shown that deep-learning is able to learn transforms that are similar to Wavelet, Fourier, or other well-known transforms. In most cases, the amount of training data that is required is in the range of millions of images. Recent work by Google even use 100’s of millions of annotated images. Another major drawback of this method is that
neither the optimal network structure can be determined prior to seeing the data, nor the trained networks can easily be interpreted. To overcome these problems several approaches have been proposed, giving some insights in the properties of the learned net. We consider this state-of-the-art to be inappropriate for future medical applications, as it stays a black box what the network has really learnt. The results obtained so far, share many properties with correlations: they show whether prediction is possible given a certain amount of data, but they do not differentiate ‘cause’ from ‘effect’. As a result, it is impossible to provide guarantees on the output of such a network given an unseen input. Today it is common to construct networks on general ideas that are often inspired by traditional signal processing and feature extraction techniques. The networks are constructed in a way that their topologies model typical feature transformation and extraction ideas. Next, the network is initialized with random weights and trained such that it learns an optimal transform with respect to the provided training data. To train ‘good’ networks, that are capable of learning complex operators, many million training samples are used. Other than artificially expanding the training data by augmentation pretraining and transfer learning there does not exist a general and stable strategy to cope with few training observations.
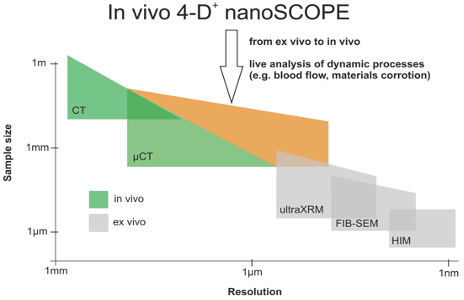
Data analytics & data life cycle
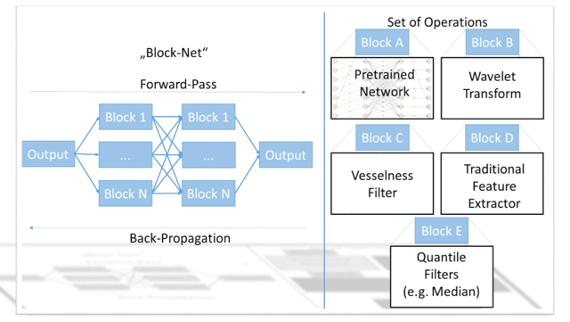In contrast to a wealth of existing literature, we do not see networks to learn operators such as Fourier and Wavelet transforms from scratch for each problem. We challenge current thinking and will use this approach of inclusion of explicit prior knowledge to training of a new network. Our approach aims at reusing known theory and operators from traditional signal processing and feature extraction methods, while only learning novel operators as sparsely as possible. We call this concept “precision learning” that we introduce in this proposal for the first time. In doing so, we use traditional methods as function blocks that can be integrated into networks without further training. Such blocks range from Fourier and Wavelet transforms to highly non-linear operators. In our prior work, we demonstrated, that all linear operators can generally be used in such a manner, even if the operator itself is too large to fit into memory. In addition, we demonstrated that we are able to learn specific new operators integrated into a chain of fixed block operators, resulting in a tremendous reduction of training data down to 10 artificial samples. Based on these observations, we are also able to integrate highly non-linear operators such as median, erosion, and dilatation filters. Although these operators do not have simple analytic gradients, the network optimization can still be solved using sub-differential theory. This approach uses the idea that even in cases in which the gradient is not unique, minimization of the optimization can still be achieved, if a valid sub-gradient direction, i.e. one of the possible gradients is followed. We demonstrated similar ideas already for the optimization of generalized quantile operators for iterative regularization that also follows a gradient-based function minimization.
- Image-based prediction of bone characteristics
First, we want to predict bone characteristics and material properties directly from image data. This forms a typical regression problem that uses feature extraction to reduce the dimensionality of the image space to predict the desired parameters. Deep learning methods can be explored on a patch-wise level training adapted transforms using auto-encoders. These can then be assembled as one of the blocks in our precision learning approach which is compared and set in comparison to other blocks based on traditional methods. Furthermore, we will also investigate image-to-image transforms that will explore whether it is possible to predict the ex-vivo images and therewith the information that experts can read from these images. One possible application for such techniques is facture prediction from image data that is also available in vivo. This opens the pathway to explore in vivo fracture analysis and prediction without the need for finite element analysis with manual fine-tuning for the first time.
- Prediction-based imaging parameter optimization
In our precision learning concept, we can also model the entire image reconstruction pipeline as a precision learning problem. Thus, we are able to optimize the imaging parameters such as number of projections and acquisition scheme with respect to the prediction of outcome parameter prediction. Doing so, we will use concepts such as sparsity injection82 to keep the number of projections low while preserving a good bone property characterization. In order to prevent images that are no longer accessible to human readers, we will incorporate high-resolution images as additional network outputs that influence the objective function. Thus, the result of the optimization will a sparsely sampled image that is still able to predict the bone and material characteristics while preserving a human-readable image. To the best of our knowledge, this is the first approach that is able to do so.
- Raw-data-based multi-modal prediction of disease outcome
In this last data analytics work package, we aim at direct prediction of disease outcome and progression from the raw image data. We expect that we will be able to find models that predict disease outcome very precisely using deep learning. The major problem of this approach is that the model will not tell us, which properties of the image are important for the prediction. Using techniques like will enable us to determine the areas that are relevant for the decision.Still, these approaches will only generate a “fuzzy” relation between the predictive area and the prediction outcome. Again, the precision learning method will help to solve this problem: By interdisciplinary discussion between medical, material, and computer science researchers, we are able to describe multi-variate hypotheses within the block-net framework. Due to their low number of parameters, we are able to verify or falsify them quickly on few training samples. Yet, the approach immediately delivers a quantitative assessment in terms of prediction accuracy. We believe that this hypothesis-driven method will generate evidence to understand the underlying processes of disease progression faster than traditional univariate approaches.